What is Expected Value?

Expected value—commonly referred to as EV—is a concept used to describe the average outcome of a given scenario that hinges on an uncertain probabilistic event.

Expected value in poker is the long-term result of your decisions in a particular poker hand.

It is your way to cut through poker’s blend of luck and strategy, so you can see how profitable your decisions are. It is not enough to only observe the result of a hand because of how variance skews your perception of how good your strategy really was.

What is EV Good for?

EV decisions are your toolbox for honing your strategies to make the most of every situation. It is not enough for you to simply choose a profitable course of action—you must strive to make the most profitable course of action available to you. Consider that your overall profit (more than just the pure amount of money that is at stake) is the total sum of every decision that you make at the poker table.

If you are playing against any opponents that are better than you, then you can expect to have a negative expectation overall. Conversely, you will be winning chips against worse players. By fighting for every single chip, you will win the most against weak players and lose the least against better players.

How to Calculate EV?

Let’s start with a non-poker example to understand its basic application, then we will move on to a poker hand example.

Suppose you are a financial analyst in a development company. Your manager just asked you to assess the viability of a future development project. According to the estimates, the project, upon completion, shows a probability of 0.4 to achieve a value of $20,000 and a probability of 0.6 to achieve a value of $50,000.

In order to obtain an estimated value of the project, you need to calculate the expected value.

EV (Project) = [0.4 * $20,000] + [0.6 * $50,000] = $38,000

Expected Value in Poker

To take an easy example, just think of how many times you’ve had pocket aces cracked after going all-in preflop. With very exceptional cases set aside (certain rare bubble and pay jump scenarios in tournaments), would you ever have considered folding those aces in hindsight?

Of course not. Because you know that getting your money in before the flop with pocket aces is a hugely profitable play in the long term.

Being a successful poker player depends on consistently making profitable (+EV) plays, many of which are more difficult to identify than others, and putting in enough volume to overcome negative variance (instances when you make the correct, +EV play, but still lose the pot), which is inevitable.

Expected Value Example

Suppose you’re on the button with $200 in a $2/4 full-ring cash game. A loose opponent opens to $16 from early position, and you call with J♦ 9♦.

Both blinds elect to fold, leaving you heads up. The pot is $38.

The flop comes 5♦ 10♦ 2♣, and your opponent fires a $30 continuation bet. You decide to call, making the pot $98, and leaving you with $154 behind.

The turn brings the 7♣. Your opponent bets $50. The pot is now $148.

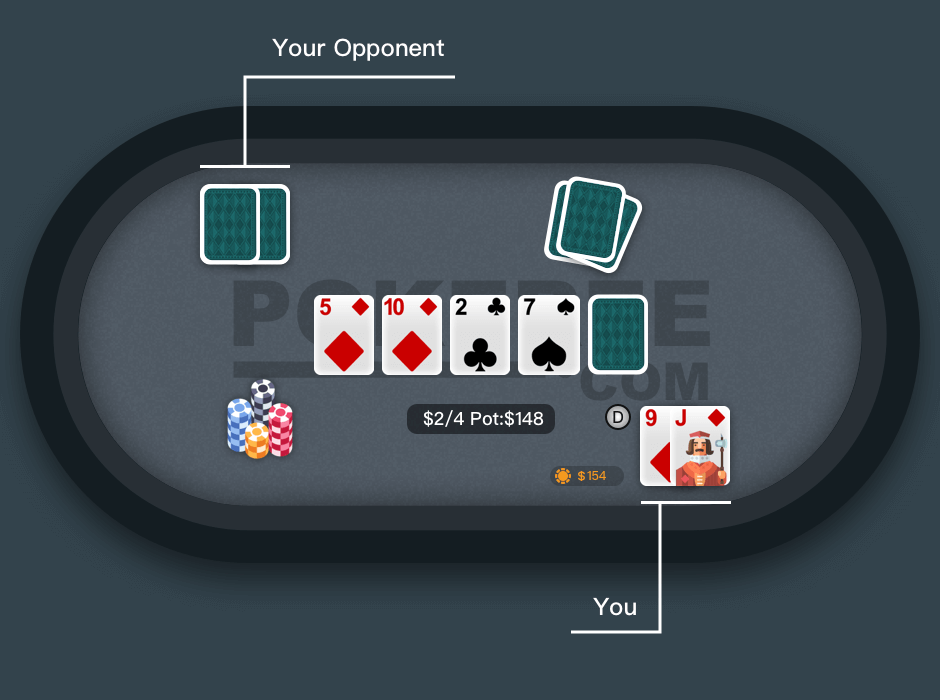
Calling is a reasonable option, but let’s consider the EV of an all-in shove.

Let’s see if this play is +EV based on the assumption that when Villain calls, it will be with a hand like T9 suited for top pair, against which your draw will have 34.09% equity.

According to the diagram, there are three possible outcomes:

1. Your opponent folds and you win $148

2. Your opponent calls and you miss your draw, you lose $154 (all in)

3. Your opponent calls and you hit your draw, you win $252 ($98 pot plus his $154)

Let’s calculate the EV for the first outcome:

EV (Fold) = $148 * 0.66 = $97.68

Now let’s calculate the EV for the second and the third outcome

Second outcome: 0.6591 * -$154 = -$101.5014

Third outcome: 0.3409 * $252 = $85.9068

EV (Call) = -$101.5014 + $85.9068 = -$15.5946

Now we can assess the play:

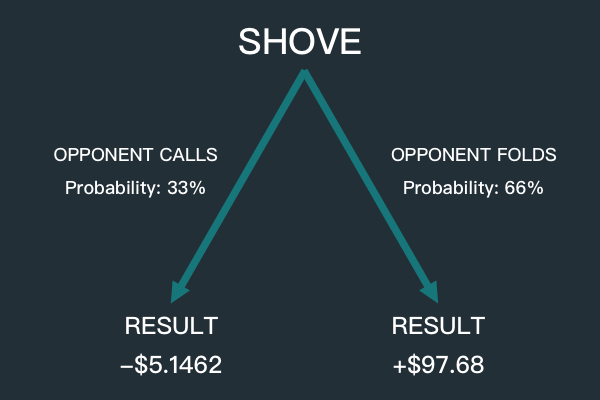
Opponent calls: 0.33 * -$15.5946 = -$5.1462

Opponent folds: 0.66 * $148 = $97.68

EV (Shove) = -$5.1462 + $97.68 = $92.5338

It is really profitable to shove!